Вероятность безотказной работы автомобиля равна 0 9

Найти вероятности всех возможных значений числа автомобилей работающих безотказно

Составить алгоритм вывода всех возможных значений натурального числа р.
Написать программу в паскале АВС, как можно быстрее, умоляю Составить алгоритм вывода всех.

Получить список всех возможных значений.
Помогите математики. Есть 42 бита, из них только 6 могут быть установлены, не больше и не меньше.

Алгоритм перебора всех возможных значений
Здравствуйте, суть задачи алгоритма состоит в поиске всех возможных сочетаний букв в слове.

Запись всех возможных значений времени
Здравствуйте, нужно записать все возможные значения времени в файл, то есть от 00:00:00,00 до.

Напишите сумму всех возможных возвращаемых значений функции
Задача. Если приведённый текст содержит синтаксические или семантические ошибки с точки зрения.

Расчет теоретических значений для всех возможных линий тренда
:umnik:Определить количество обработанных деталей, которое можно выполнить заданным инструментом до.

Брутфорс (вывод всех возможных значений строки для заданного алфавита)
Доброго времени суток! У меня имеется брутфорс и он вроде как даже рабочий, но возникла.

Вывод всех возможных делителей числа
Пишу программу, которая выводит из введённого числа его возможные делители. Число должно делится на.

Источник

Вероятность безотказной работы автомобиля равна 0 9

Как получить объективную картину по ссылочному индексу и не переплачивать за данные

В Яндексе выяснили, каким городам России чаще везет с погодой на Новый год

Необходимо решить 7 задач по терверу, результат: точный ответ и ход решения. Задачи простые

1. Сколько шестизначных чисел можно образовать из цифр 1,2,3,4,5,6,7,8,9, если каждое число должно состоять из трех четных и трех нечетных цифр, причем никакая цифра не входит в число более одного раза?

2. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при условии, что все они должны ехать в различных вагонах?

3. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делигацию из трех человек. Найти вероятность того, что в делегацию войдут две женщины и один мужчина.

5. Читатель разыскивает книгу в трех библиотеках. Одинакова вероятно, есть или нет в фонде очередной библиотеки кника и так же одинаково вероятно, выдана она или нет. Чему равна вероятность того, что читатель найдет нужную книгу?

7. На фабрике машины a,b,c производят соответственно 20%, 35%, 45% всех изделий. В их продукции брак составляет 3%, 2%, 4%. Какова вероятность того, что случайно выбранноен дефектное изделие произведено a,b,c соответственно?

Нужны до 6 утра по москве завтрашнего дня.

Решения выкладывайте здесь или кидайте в асю, если препод примет обязательно оплачу, не примет, компенсирую умственные затраты.

Источник

Задачи для самостоятельного решения. 1. Круговая мишень состоит из трех зон

1. Круговая мишень состоит из трех зон. Вероятности попадания а эти зоны при одном выстреле соответственно равны: 0,1; 0,35 и 0,4. Найти вероятность:

а) попадания в первую или третью зоны;

б) промаха по мишени.

2. Вероятность поражения первой мишени для данного стрелка равна 0,6. Если при первом выстреле зафиксировано попадания, то стрелок получает право на следующий выстрел по второй мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,3. Определить вероятность поражения второй мишени.

3. В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из вызванных наудачу трех студентов:

б) первые две девушки, третий – юноша;

4. Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производят по одному до первого попадания. Определить вероятность того, что придется производить четвертый выстрел.

5. Вероятность безотказной работы автомобиля равна 0,9. Автомобиль перед выходом на линию осматривается двумя механиками. Вероятность того, что первый механик обнаружит неисправность в автомобиле, равна 0,8, а второй – 0,9. Если хотя бы один механик обнаружит неисправность, то автомобиль отправляется на ремонт. Найти вероятность того, что:

а) автомобиль будет выпущен на линию;

б) автомобиль не будет выпущен на линию.

6. Вероятность одного попадания в цель при одновременном залпе из двух орудий равна 0,44. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.

7. Из 40 деталей 5 бракованных. Какова вероятность того, что взятые одновременно две детали не будут бракованными.

8. В коробке 12 карандашей трех цветов, по четыре карандаша каждого цвета. Наудачу вынимают три карандаша. Найти вероятность того, что все карандаши окажутся разного цвета. Решить задачу при условии:

а) карандаши возвращают в коробку;

б) карандаши не возвращают в коробку.

9. Из урны, содержащей четыре красных и шесть черных шаров, вынимают два шара (без возвращения первого). Какова вероятность того, что будут вынуты:

а) два шара черного цвета;

б) красный и черный в любой последовательности;

в) второй шар будет черным;

г) оба шара одного цвета.

10. Вероятность выигрыша по лотерейному билету равна 0,1. Приобретено три билета. Какова вероятность выиграть хотя бы по одному из них?

11. Вероятность попадания в цель при стрельбе из орудия равна 0,6. Производится по одному выстрелу одновременно из трех орудий. Цель будет поражена, если в нее попадут не менее двух орудий. Найти вероятность:

б) промаха одним или двумя орудиями.

12. Слово «машина» составлено из букв разрезной азбуки. Какова вероятность того, что, перемешав все буквы и укладывая их в ряд по одной, получим слово:

13. В магазин вошли три покупателя. Вероятность того, что каждый что-нибудь купит, равна 0,3. Найти вероятность того, что:

а) два из них совершат покупки;

б) все три совершат покупки;

в) ни один не совершит покупки;

г) хотя бы один купит товар.

14. Вероятность получить высокие дивиденды по акциям на первом предприятии – 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды:

а) на всех предприятиях;

б) только на одном предприятии;

в) хотя бы на одном предприятии.

15. Брошены две игральные кости. Предполагается, что все комбинации выпавших очков равновероятны. Найти условную вероятность того, что выпали две пятерки, если известно, что сумма выпавших очков делится на пять.

16. Два игрока поочередно бросают две игральные кости. Выигрывает первый, у которого в сумме появится 12 очков. Найти вероятность выигрыша каждого игрока.

17. Через автобусную остановку проходят автобусы семи маршрутов с равной частотой. Пассажир ожидает автобус одного из маршрутов №1, №5, №7. Какова вероятность того, что нужный ему автобус будет одним из первых трех подошедших к остановке?

18. Читатель в поисках нужной книги обходит три библиотеки. Вероятность того, что она имеется в очередной библиотеке, равна 0,3. Что вероятнее: найдет читатель книгу или нет?

19. В денежно-вещевой лотереи на каждые 1000 билетов приходится 12 денежных и 8 вещевых выигрышей. Какова вероятность выигрыша хотя бы на один из трех приобретенных билетов?

20. Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично» равна для первого студента 0,7, для второго – 0,6, для третьего – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»:

а) только одним из студентов;

б) двумя студентами;

21. Первый студент из 20 вопросов программы выучил 17, второй – 12. Каждому студенту задают по одному вопросу. Определить вероятность того, что:

а) оба студента правильно ответят на вопрос;

б) хотя бы один ответит на вопрос;

в) правильно ответит только первый студент.

22. Студент из 40 экзаменационных вопросов выучил только 30. Каким выгодней ему зайти на экзамен, первым или вторым?

23. Сколько раз необходимо бросить игральную кость, чтобы с вероятностью 0,9 хотя бы один раз выпало не менее четырех очков?

Источник

Примеры решения задач контрольного задания

Примеры решения задач контрольного задания

Задача 1: Определить показатель Рс надежности ИС, содержащей 4 элемента и имеющей следующую ССН:

Решение. Поскольку в ИС элементы 1 и 3 соединены последовательно в смысле надежности (отказ любого элемента приводит к отказу всей этой цепочки элементов), то показатель их общей надежности Р13=Р1*Р3 (принцип “ цепь не крепче ее наислабейшего звена”). Аналогично Р24=Р2*Р4. Теперь эквивалентная ССН ИС содержит 2 элемента и имеет следующий эквивалентный вид:

Определить для указанной выше ИС вероятность безотказной работы Рс за заданное время, если вероятности безотказной работы ее элементов за это время составляют Р1= 0.9, Р2= 0.8, Р3= 0.9, Р4= 0.8.

Решение. Используя формулу (П1), имеем Рс = 1 – (1 – 0.81) * (1 – 0.64) =

= 1 –0.19 * 0.36 = = 1 – 0.0684 = 0.9316.

[При подготовке к зачёту самостоятельно подготовьтесь к решению задач по оценке надежности ИС по их структурным схемам надежности при различном числе элементов ИС (N=2,3,4,5)].

Задача 2: Поток отказов ИС подчинен закону Пуассона с параметром l=0.0001 1/час. Определить вероятность того, что за время с момента начала работы в течение t1 час ИС будет работоспособна, а в течение t2 час в ней не будет более N отказов. Пусть задано t1 = 1000 час; t2 = 1 год; N = 2.

Решение. В соответствии с законом Пуассона вероятность возникновения ровно К отказов за время t при простейшем потоке отказов с параметром l определяется следующей формулой:

. (П2)

Следовательно, вероятность того, что за время с момента начала работы в течение 1000 час ИС будет работоспособна (число отказов К =0), равна:

0,905.

Аналогично за время t2 = 1 год = 8760 час имеем:

Ро(8760)= exp(–0.0001*8760) 0,416.

В случае К =1 в соответствии с (П2) определим Р1(8760):

0,876*0,416 ≈ 0,364.

При К =2 в соответствии с (П2) определим Р2(8760):

0,384*0,416 ≈ 0,160.

Источник

ОСНОВНЫЕ ТЕОРЕМЫ И ИХ СЛЕДСТВИЯ

Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

. (2.1)

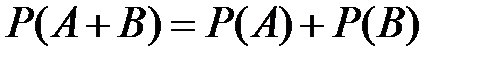
Для n несовместных событий теорема имеет вид:

. (2.2)

Следствие 1. Сумма вероятностей несовместных событий, образующих полную группу событий, равна 1.

Следствие 2. Сумма вероятностей противоположных событий равна 1:

или p + q = 1. (2.3)

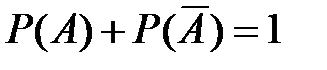
Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

. (2.4)

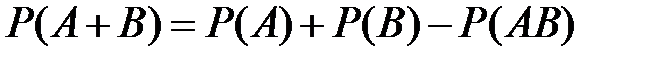
События называются независимыми, если появление одного из них не изменяет вероятности появления другого события.

Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух или нескольких независимых событий равна произведению вероятностей этих событий:

; . (2.5)

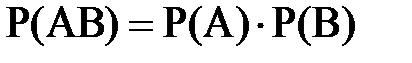
Теорема умножения вероятностей зависимых событий. Вероятность произведения двух зависимых событий равна произведению вероятности наступления первого события на условную вероятность второго события при условии, что первое событие уже наступило:

; (2.6) . (2.7)

Теорема наступления хотя бы одного из событий. Вероятность наступления хотя бы одного из событий А₁, А₂, …, А_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :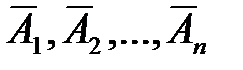

. (2.8)

Следствие. Если события А_i имеют одинаковую вероятность появиться р, то вероятность появления хотя бы одного события из n независимых событий:

, где р + q = 1. (2.9)

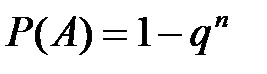
Формула волной вероятности. Пусть событие А может появиться вместе с одним из попарно несовместных событий 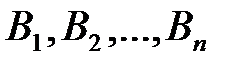образующих полную группу событий. Будем называть события гипотезами для события А. Тогда вероятность наступления события А определяется по формуле:

, (2.10)

. (2.11)

, (2.12)

, (2.13)

где 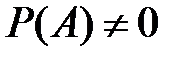— находится по формуле полной вероятности.

1Производится три выстрела по мишени. Рассматриваются события: А₁ – попадание в цель первым выстрелом; А₂ – попадание в цель вторым выстрелом; А₃ – попадание в цель третьим выстрелом. Определить, каким событиям равносильны следующие события: 1) ; 2) ;

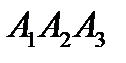
3) ; 4) ; 5) ; 6) ;

7) ; 8) ; 9) .

2Монета подбрасывается три раза. Рассматриваются события А_i – появление герба при – ом подбрасывании . Представить в виде сумм, произведений и сумм произведений событий A_i и следующие события: — появились все три герба; — появились все три цифры; — появился хотя бы один герб; — появилась хотя бы одна цифра; — появился только один герб; — появилась только одна цифра.

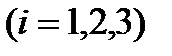
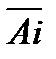
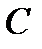
3Круговая мишень состоит из трех зон. Вероятности попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35 и 0,4. Найти вероятность: а) попадания в первую или третью зоны; б) промаха по мишени.

4Вероятность поражения первой мишени для данного стрелка равна 0,6. Если при первом выстреле зафиксировано попадание, то стрелок получает право на следующий выстрел по второй мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,3. Определить вероятность поражения второй мишени.

6Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производятся по одному до первого попадания. Определить вероятность того, что придется производить четвертый выстрел.

7Вероятность безотказной работы автомобиля равна 0,9. Автомобиль перед выходом на линию осматривается двумя механиками. Вероятность того, что первый механик обнаружит неисправность, равна 0,8, а второй – 0,9. Если хотя бы один механик обнаружит неисправность, то автомобиль отправляется в ремонт. Найти вероятность того, что: а) автомобиль будет выпущен на линию; б) автомобиль не будет выпущен на линию.

8Вероятность одного попадания в цель при одновременном залпе из двух орудий 0,38. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.

9Из 40 деталей в ящике 5 бракованных. Какова вероятность того, что взятые две детали не будут бракованными?

10В коробке 12 карандашей трех цветов, по четыре карандаша каждого цвета. Наудачу последовательно вынимают три карандаша. Найти вероятность того, что все карандаши окажутся разного цвета. Решить задачу при условии: а) карандаши возвращают в коробку; б) карандаши не возвращают в коробку.

11Из урны, содержащей четыре красных и шесть черных шаров, вынимают два шара (без возвращения первого). Какова вероятность того, что будут вынуты: а) оба шара черного цвета; б) красный и черный в любой последовательности; в) второй шар будет черным; г) оба шара одного цвета?

12Вероятность выигрыша по лотерейному билету равна 0,1. Приобретено три билета. Какова вероятность выиграть хотя бы по одному из них?

13Вероятность попадания в цель при стрельбе из орудия равна 0,6. Производится по одному выстрелу одновременно из трех орудий. Цель будет поражена, если в нее попадут не менее двух орудий. Найти вероятность: а) поражения цели; б) промаха одним или двумя орудиями.

14Слово «машина» составлено из букв разрезной азбуки. Какова вероятность того, что перемешав буквы и укладывая их в ряд по одной, получим слово: а) «машина»; б) «шина»; в) «маша»?

15В магазин вошли три покупателя. Вероятность того, что каждый что-нибудь купит, равна 0,3. Найти вероятность того, что: а) два из них совершат покупки; б) все три совершат покупки; в) ни один не совершит покупки; г) по крайней мере два совершат покупки; д) хотя бы один купит товар.

16Вероятность получить высокие дивиденды по акциям на первом предприятии – 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.

17В продаже имеется 12 акций одного предприятия, 8 другого и 10 третьего. Клиент покупает три акции. Найти вероятность того, что клиентом будут куплены: а) акции одного предприятия; б) все три акции разных предприятий.

18Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым появится шесть очков. Найти вероятность выигрыша для каждого игрока.

19Через автобусную остановку проходят автобусы семи маршрутов с равной частотой. Пассажир ожидает автобус одного из маршрутов №1, №5, №7. Какова вероятность, что нужный ему автобус будет одним из первых трех подошедших к остановке?

20Читатель в поисках нужной книги обходит три библиотеки. Вероятность того, что она имеется в очередной библиотеке равна 0,3. Что вероятнее – найдет читатель книгу или нет?

21В денежно-вещевой лотерее на каждые 1000 билетов приходится 12 денежных и 8 вещевых выигрышей. Какова вероятность выигрыша хотя бы на один из трех приобретенных билетов?

22В урне 10 красных, 5 зеленых и 3 черных шара. Определить вероятность того, что взятые наудачу два шара будут: а) одного цвета; б) разных цветов.

23На базу поступило 40 ящиков овощей, из них 30 первого сорта. Наудачу для проверки берут два ящика. Какова вероятность, что оба содержат овощи: а) первого сорта; б) разного сорта; в) одного сорта?

24Читатель разыскивает книгу в трех библиотеках. Одинаково вероятно, есть или нет в фонде очередной библиотеки книга и также одинаково вероятно, выдана она или нет. Чему равна вероятность того, что читатель найдет нужную книгу?

26Первый студент из 20 вопросов программы выучил 17, второй – 12. Каждому студенту задают по одному вопросу. Определить вероятность того, что: а) оба студента правильно ответят на вопрос; б) хотя бы один ответит верно; в) правильно ответит только первый студент.

27Сколько раз необходимо бросить игральную кость, чтобы с вероятностью 0,9 хотя бы один раз выпало не менее четырех очков?

28В первой бригаде 6 тракторов, во второй – 9. В каждой бригаде один трактор требует ремонта. Из каждой бригады наудачу выбирают по одному трактору. Какова вероятность того, что: а) оба трактора исправны; б) один требует ремонта; в) трактор из второй бригады исправен.

29На предприятии имеется три автомобиля. Вероятность безотказной работы первого из них равна 0,9, второго – 0,7, третьего – 0,8. Найти вероятности всех возможных значений числа автомобилей, работающих безотказно в течение определенного времени.

30Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,784. Найти вероятность одного промаха при трех выстрелах.

31В круг радиуса R вписан прямоугольник наибольшей площади. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся внутри заданного прямоугольника?

32В шар радиуса R вписан прямой конус наибольшего объема. Чему равна вероятность того, что из поставленных наудачу внутри шара двух точек хотя бы одна окажется внутри конуса.

33Вероятность спортсменом взять в одной попытке высоту 1,8 м равна 0,6, высоту 2 м – 0,2, высоту 2 м 10 см – 0,1. Спортсмен, не взявший предыдущую высоту, выбывает из соревнований. Спортсмену на каждую высоту дается три попытки. Определить вероятность того, что спортсмен закончит соревнования, взяв высоту: а) 1,8 м; б) 2 м; в) 2 м 10 см.

34В первой урне 5 красных, 3 белых и 2 черных шара. Во второй 3 белых и 2 черных шара. Из первой урны взято 2 шара, а из второй один. Определить вероятность того, что среди них: а) все шары одного цвета; б) все шары разного цвета.

35При исследовании жирности молока коров все стадо было разбито на три группы. В первой группе оказалось 70%, во второй 23% и в третьей 7% всех коров. Вероятность того, что молоко, полученное от отдельной коровы имеет не менее 4% жирности, для каждой группы коров соответственно равна 0,6; 0,4 и 0,1. Определить вероятность того, что для взятой наудачу коровы жирность молока составит не менее 4%. Взятая наудачу корова дает молоко жирностью не менее 4%. Найти вероятность того, что эта корова из первой группы.

36В первой урне 10 деталей, из них 8 стандартных. Во второй 6 деталей, из которых 5 стандартных. Из второй урны переложили в первую одну деталь. Какова вероятность того, что деталь, извлеченная после этого из второй урны, нестандартная?

37Имеются две урны. В первой – семь красных шаров и три черных, во второй – три красных и четыре черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным.

39Предприятие использует для производства продукта сырье трех других предприятий. Объем поступающего сырья относится в пропорции 1: 2: 5. Известно, что первое предприятие поставляет 60 % сырья высокого качества, второе 70 % и третье 90 %. Случайно взятая единица сырья оказалась высокого качества. Найти вероятность того, что она поступила от второго или третьего предприятия.

40В первом ящике из 20 деталей 4 бракованных, во втором из 30 деталей 5 бракованных. Из первого во второй переложили две детали. Найти вероятность того, что деталь, извлеченная после этого из второго ящика, бракованная.

43Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно вызванный студент ответил на два заданных вопроса. Какова вероятность, что он из тех трех студентов, которые подготовили по 10 вопросов?

44Запасная деталь может находиться в одной из трех партий с вероятностями p₁ = 0,2; p₂ = 0,5; p₃ = 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8 и 0,7. Определить вероятность того, что: а) взятая наудачу деталь проработает положенное время; б) деталь, проработавшая положенное время, взята из второй или третьей партии.

45Имеется 5 урн. В первой, второй и третьей находится по 4 белых и 6 черных шаров, в четвертой и пятой урнах по 2 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что была выбрана четвертая или пятая урна, если извлеченный шар оказался белым?

46В первой бригаде производится в три раза больше продукции, чем во второй. Вероятность того, что производимая продукция окажется стандартной для первой бригады, равна 0,7, для второй – 0,8. Определить вероятность того, что взятая наугад единица продукции будет стандартной. Взятая наугад единица продукции оказалась стандартной. Какова вероятность, что она из второй бригады?

Источник